Колебания – это движения или процессы, которые характеризуются определенной повторяемостью во времени.

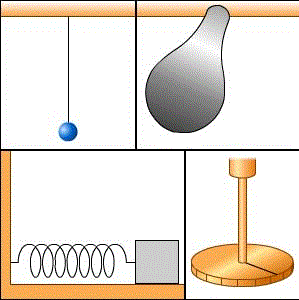
Рис. 1. Различные колебательные процессы

Период колебаний T – интервал времени, в течение которого происходит одно полное колебание.

Частота колебаний ν – число полных колебаний в единицу времени. В системе СИ выражается в герцах (Гц).

Период и частота колебаний связаны соотношением:

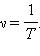Циклическая частота ω = 2πν. Она связана с периодом отношением:

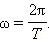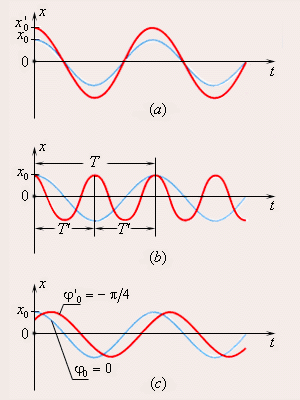
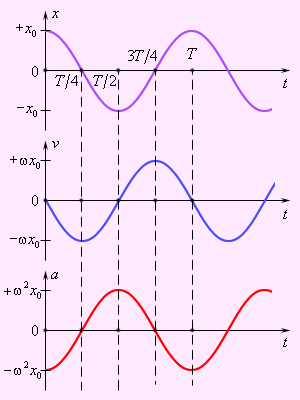
Гармонические колебания – это колебания, при которых колеблющаяся величина, например смещение груза на пружине от положения равновесия, изменяется по закону синуса или косинуса: где x₀ – амплитуда, ω – циклическая частота, φ₀ – начальная фаза колебания.

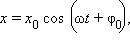Ускорение при гармонических колебаниях всегда направлено в сторону, противоположную смещению; максимальное ускорение равно по модулю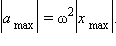

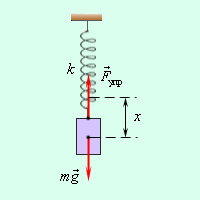
Рис. 2. Амплитуда, частота и фаза колебаний. a) Колебания с различными амплитудами. b) Колебания с различными периодами. c) Колебания с различной начальной фазой. Рис. 3. Смещение, скорость и ускорение гармонических колебаний

В качестве примеров свободных колебаний можно привести пружинный и математический маятники. Пружинный (гармонический) маятник – груз массы m, прикрепленный к пружине жесткости k, второй конец которой закреплен неподвижно. Циклическая частота колебаний груза равна: а период:

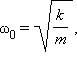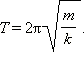Рис. 4. Пружинный маятник

Математический маятник – тело небольших размеров, подвешенное на тонкой нерастяжимой невесомой нити длиной l. Циклическая частота математического маятника равна: а период колебаний:

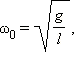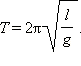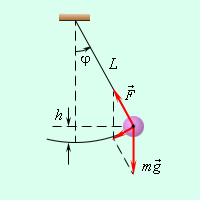Рис. 5. Математический маятник

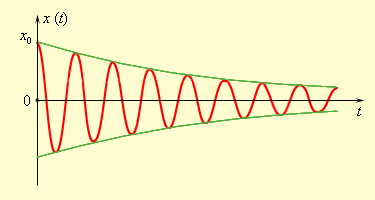
В реальных условиях любая механическая система находится под действием сил трения (сопротивления). При этом часть механической энергии превращается во внутреннюю энергию теплового движения, и колебания становятся затухающими.

Рис. 6. График затухающих колебаний

Вынужденные колебания – колебания, возникающие под действием внешней периодически изменяющейся силы. Частота вынужденных колебаний равна частоте изменения внешней силы.

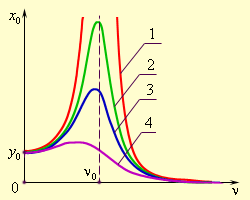
Если частота ν внешней силы совпадет с частотой свободных колебаний системы, то амплитуда колебаний резко возрастает. Это явление называется резонансом. В колебательных системах с затуханием значение резонансной частоты смещается в сторону более низких частот (рис. 7).

Рис. 7. Чем меньше трение, тем больше амплитуда резонансных колебаний и тем острее пик на резонансной кривой

Автоколебания – это незатухающие свободные колебания, поддерживаемые за счет периодической подкачки энергии от какого-либо источника внешней силы. Примером автоколебательной системы могут служить механические часы.